Licence de Mathématique - Faculté des Sciences Jean Perrin - Université d'Artois
 Licence de Mathématiques
Licence de Mathématiques 
La Licence de Mathématiques est une formation sur trois années après le baccalauréat, dont la première année est largement commune avec la Licence d'Informatique . L'objectif principal de la formation est de permettre l'acquisition de connaissances solides dans toutes les branches classiques des mathématiques (algèbre, géométrie, analyse, probabilités). Parallèlement, les étudiants apprennent un langage de programmation et se familiarisent avec un logiciel de calcul scientifique. Tous les enseignements ont lieu à Lens, sur le site de la Faculté des Sciences Jean Perrin |
|

Organisation de la Formation
La formation est organisée sur six semestres.
Les deux premiers semestres sont fortement mutualisés avec la licence d'informatique (possibilité de bifurquer de l'une vers l'autre licence à la fin du premier ou du deuxième semestre).
Le contenu mathématique des 2 premières années est très comparable à celui des classes préparatoires scientifiques (MPSI, MP*). En 3ème année, on va bien entendu beaucoup plus loin.
En 2ème année, les étudiants qui le souhaitent peuvent effectuer un stage dans un établissement d'enseignement primaire ou secondaire.
Un stage est prévu en 3ème année : stage en établissement d'enseignement primaire ou secondaire, stage de type « recherche » , ou stage en entreprise .
Compétences Acquises
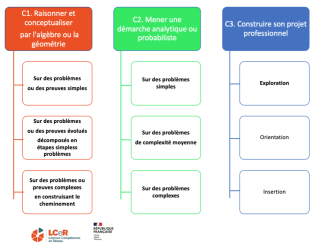
Référentiel de Compétences
Licence de Mathématiques : Niveaux de compétences par année
Positionnez la souris (ou cliquez) sur l'icône ⓘ pour faire apparaître plus de détails
Semestre 1 |
ECTS |
Semestre 2 |
ECTS |
|||
Compétence 1
|
UE 1-1 |
9 |
UE 1-2 |
7 |
||
| Raisonner et conceptualiser par l'algèbre ou la géométrie
|
Méthodes et Outils pour les Mathématiques et l'Informatique : MOMI ⓘ Compétences visées |
9 |
Algèbre Linéaire 1 ⓘ
|
7 | ||
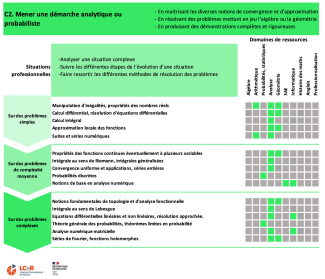
Compétence 2
|
UE 2-1 |
8 |
|
UE 2-2 |
13 |
|
|
Mener une démarche analytique ou probabiliste |
Calculus 1 ⓘ Compétences Visées |
8 |
Nombres réels, suites et séries (année L1) ⓘ
|
7 |
||
|
Calculus 2 ⓘ
|
6 | |||||
Compétence 3
|
UE 3-1 |
13 |
|
UE 3-2 |
10 |
|
|
Construire son projet professionnel |
Anglais 1 ⓘ Les unités se déroulent uniquement sous forme de TD. A chaque séance, les «compétences» suivantes seront systématiquement cultivées. |
3 |
Anglais 2 ⓘ Les unités se déroulent uniquement sous forme de TD. A chaque séance, les «compétences» suivantes seront systématiquement cultivées. |
3 |
||
|
Algorithmique et Programmation 1 ⓘ L'objectif de cette unité est de faire acquérir aux étudiants des notions et concepts de base de la programmation impérative. Seront abordés : |
7 |
Algorithmique et Programmation 2 ⓘ
|
5 | |||
|
Projet Professionnel et Personnel de l'Etudiant.e ⓘ Cette unité a pour but de permettre à l'étudiant d'enclencher une démarche de réflexion active sur son orientation et sa future insertion professionnelle. |
3 |
SAE Projet Algo | 2 | |||
Positionnez la souris (ou cliquez) sur l'icône ⓘ pour faire apparaître plus de détails
Semestre 3 |
ECTS |
Semestre 4 |
ECTS |
|||
Compétence 1
|
UE 1-3 |
10 |
UE 1-4 |
14 |
||
| Raisonner et conceptualiser par l'algèbre ou la géométrie
|
Algèbre ⓘ
|
5 |
Algèbre Linéaire L2 ⓘ
|
8 | ||
|
Produits scalaires et formes quadratiques ⓘ
|
5 |
Géométrie ⓘ
|
6 | |||
Compétence 2
|
UE 2-3 |
17 |
|
UE 2-4 |
12 |
|
|
Mener une démarche analytique ou probabiliste |
Probabilités L2 ⓘ
|
5 |
|
Fonctions de plusieurs variables ⓘ
|
7 |
|
|
Analyse numérique L2 ⓘ
|
3 |
Suites et séries de fonctions ⓘ
|
5 | |||
|
Fonctions d'une variable réelle ⓘ
|
7 | |||||
| SAE Analyse numérique L2 |
2 |
|
||||
Compétence 3
|
UE 3-3 |
3 |
|
UE 3-4 |
4 |
|
|
Construire son projet professionnel |
Anglais 3 ⓘ
|
3 |
Anglais 4 ⓘ
|
3 |
||
|
|
Culture numérique 2 ⓘ
|
1 | ||||
Positionnez la souris (ou cliquez) sur l'icône ⓘ pour faire apparaître plus de détails
Semestre 5 | ECTS | Semestre 6 | ECTS | |||
Compétence 1 | UE 1-5 | 8 | UE 1-6 | 6 | ||
Raisonner et conceptualiser par l'algèbre ou la géométrie
| Groupes et anneaux ⓘ
| 8 | Corps et graphes ⓘ
| 6 | ||
Compétence 2 | UE 2-5 | 14 | UE 2-6 | 12 | ||
| Mener une démarche analytique ou probabiliste | Espaces vectoriels normés et topologie ⓘ
| 7 | Probabilités L3 ⓘ
| 6 | ||
Théorie de l'intégration ⓘ
| 7 | Séries de Fourier et analyse complexe ⓘ
| 6 | |||
Compétence 3 | UE 3-5 | 8 | UE 3-6 | 12 | ||
| Construire son projet professionnel | Anglais 5 ⓘ
| 3 | Anglais 6 ⓘ
| 3 | ||
1 option parmi 2 :
| 5 | 1 option parmi 2 :
| 5 | |||
| Stage ⓘ
| 4 | ||||
Débouchés et poursuite d'études
La formation est conçue de façon à permettre une poursuite d'études couronnée de succès
- dans n'importe quel Master à dominante mathématique;
- dans un Master préparant aux métiers de l'enseignement : professeur des écoles / professeur certifié en mathématiques / Professeur agrégé en mathématiques
Pour un aperçu des nombreux débouchés possibles après des études de mathématiques, on pourra par exemple consulter la brochure ONISEP consacrée aux métiers des Mathématiques, de la Statistique et de l'Informatique.